Timing Diagram (Part 4 - Timing Diagrams Comparison using Motion Simulation in Microsoft Excel)
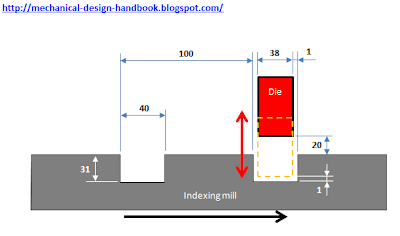
In post [ Timing Diagram (Part 1 - No Overlap Movement) ], we saw the design requirement that we have to design the die to work together with the indexing mill with the construction as shown below. Without detailed calculation, we could end up with a very simple timing diagram as shown below. But it's not good enough. The die has to wait for the indexing to finish its movement before moving. This reduces the indexing time of the die, and get high acceleration on the die. In post [ Timing Diagram (Part 2 - Maximum acceleration calculation) ], we calculated the maximum acceleration of Cycloidal motion cam profile and saw the opportunity to reduce the acceleration by extending the indexing time. In post [ Timing Diagram (Part 3 - Cycloid Cam Profile Analysis) ], we analyzed the cycloid cam profile and see opportunity of overlap motion. Some calculations have been made and we end up with new timing diagram which is smarter than the original one as shown below. We calculat


